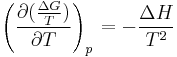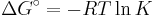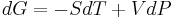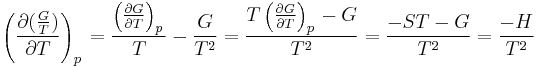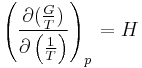Gibbs–Helmholtz equation
The Gibbs–Helmholtz equation is a thermodynamic equation useful for calculating changes in the Gibbs energy of a system as a function of temperature. It is named after Josiah Willard Gibbs and Hermann von Helmholtz:
With:
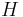 the enthalpy
the enthalpy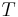 the absolute temperature
the absolute temperature the Gibbs free energy
the Gibbs free energy
at constant pressure 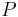 . The equation states that the change in the G/T ratio at constant pressure as a result of an infinitesimally small change in temperature is a factor (H/T2).
. The equation states that the change in the G/T ratio at constant pressure as a result of an infinitesimally small change in temperature is a factor (H/T2).
For a chemical reaction the equation reads:
with 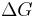 as the change in Gibbs energy and
as the change in Gibbs energy and  as the enthalpy change (which is considered independent of temperature).
as the enthalpy change (which is considered independent of temperature).
which can rearrange to:
This equation quickly enables the calculation of the Gibbs free energy change for a chemical reaction at any temperature T2 with knowledge of just the Standard Gibbs free energy change of formation and the Standard enthalpy change of formation for the individual components at 25°C and 1 bar.
Through:
which relates Gibbs energy to an equilibrium constant, the van 't Hoff equation is derived.
Proof
The Gibbs free energy for a closed system
at constant pressure 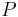 (dP = 0) reduces to
(dP = 0) reduces to
or
The dependence of the G/T ratio on T is found with the aid of the quotient rule:
Sometimes it can be found like this:
Here, the chain rule has been used with a bit of rearrangement. If  and
and  are functions of
are functions of  , the chain rule says that
, the chain rule says that 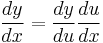 . Dividing both sides through by
. Dividing both sides through by  gives
gives  . In the equation above,
. In the equation above,  is
is  ,
,  is
is  , and u is
, and u is  . Thus,
. Thus,  is
is  .
.